Data una funzione $f$, sappiamo che in certi casi è possibile determinare la funzione inversa $f^{-1}$. Questa funzione, sostanzialmente, agisce come $f$ ma “al contrario”: se $f(a) = b$, allora $f^{-1}(b) = a$, per ogni scelta di $a, b$ opportuni. Purtroppo, però, non sempre è possibile determinare la funzione inversa di una funzione $f$ arbitraria. La situazione più problematica si incontra quando la funzione considerata non è iniettiva: tentando di invertire una funzione non iniettiva, infatti, si finisce a considerare una relazione che non è nemmeno una funzione!
Questa è in effetti la situazione in cui ci troviamo quando tentiamo di invertire le funzioni goniometriche elementari, ovvero le funzioni $$\sin(x), \quad \cos(x), \quad \tan(x), \quad \cot(x)$$Le funzioni goniometriche, infatti, sono ben lontane dall’essere iniettive: per esempio esistono infiniti valori di $x$ per cui l’equazione goniometrica elementare $\sin(x) = \frac{1}{2}$ è verificata, come $x = \frac{\pi}{6} + 2k\pi$ al variare di $k \in \mathbb{Z}$. Come possiamo procedere in questo caso?
Riflettendo un momento, ci rendiamo conto che il problema di fondo è questo: la relazione $f^{-1}$ che otteniamo invertendo una funzione non iniettiva associa “troppi elementi” all’elemento dal quale partiamo. In altre parole, l’insieme $f^{-1}(b)$ con $f$ non iniettiva è costituito da più di un elemento, e affinché $f^{-1}$ sia una funzione bisogna avere a che fare con insiemi $f^{-1}(b)$ costituiti da un solo elemento, per ogni scelta di $b$. Nel caso di una funzione goniometrica elementare $g$, la situazione è addirittura “patologica”: $g^{-1}(b)$ è sempre costituito da infiniti elementi, per ogni scelta di $b$ nel codominio di $g$.
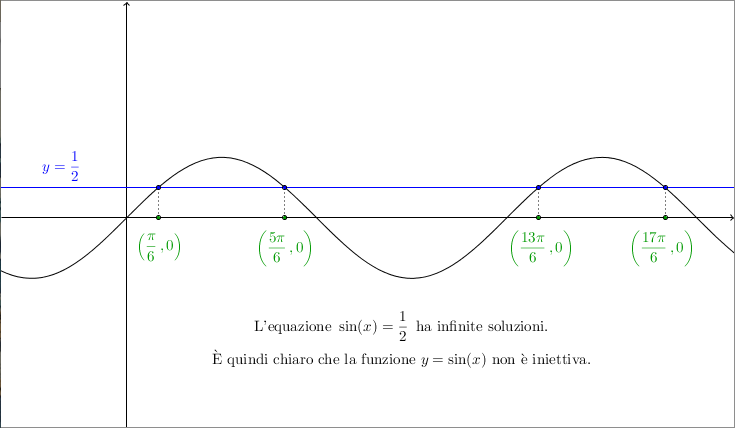
Iniziamo a capire come invertire la funzione $\sin(x)$. Questa funzione associa a un valore in $\mathbb{R}$ un numero nell’intervallo $[-1, 1]$; quindi la funzione inversa che vogliamo definire dovrà associare a un numero in $[-1, 1]$ un unico numero in $\mathbb{R}$. Come facciamo a sceglierlo? Di solito, si usa la seguente definizione.
Definizione
Chiamiamo arcoseno una delle “possibili funzioni inverse” di $\sin(x)$, definita in questo modo: $$\arcsin: [-1, 1] \rightarrow \left [ -\frac{\pi}{2}, \frac{\pi}{2} \right ]$$In altre parole, $\alpha = \arcsin(t)$ è quell’angolo compreso tra $-\frac{\pi}{2}$ e $\frac{\pi}{2}$ che soddisfa la relazione $\sin(\alpha) = t$.
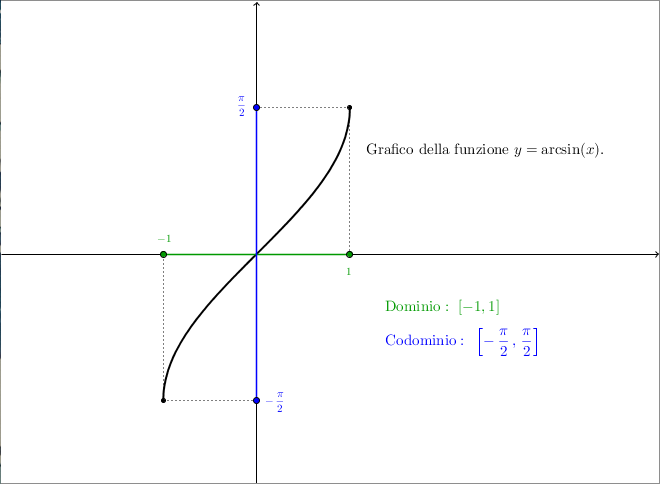
L’intervallo $\left [ -\frac{\pi}{2}, \frac{\pi}{2} \right ]$ è stato scelto apposta in modo tale che l’angolo $\alpha$ il cui seno sia $t$ sia unico (questo si verifica facilmente osservando la circonferenza goniometrica). Potevamo sicuramente scegliere altri intervalli (come per esempio $\left [ \frac{\pi}{2}, \frac{3\pi}{2} \right ]$) ma in genere si sceglie l’intervallo indicato nella definizione.
Un’altra notazione in uso per la funzione $\arcsin(x)$ è $\sin^{-1}(x)$, utilizzata di solito per sottolineare che tale funzione è proprio l’inversa della funzione seno.
Seguendo un ragionamento analogo al precedente, possiamo definire anche la funzione inversa di $\cos(x)$:
Definizione
Chiamiamo arcocoseno la funzione definita come$$\arccos: [-1, 1] \rightarrow \left [ 0, \pi \right ]$$tale per cui $\alpha = \arccos(t)$ è quell’angolo compreso tra $0$ e $\pi$ che soddisfa la relazione $\cos(\alpha) = t$.

Anche in questo caso la scelta del codominio dell’arcocoseno è del tutto arbitraria, ma per convenzione si sceglie l’intervallo $\left [ 0, \pi \right ]$.
Una notazione alternativa in uso per la funzione $\arccos(x)$ è $\cos^{-1}(x)$ (similmente a quanto accade per la funzione arcoseno).
Per invertire la funzione $\tan(x)$ procediamo nella stessa maniera seguita prima. Sappiamo che esistono infiniti angoli che hanno tangente pari a $t$, dove $t \in \mathbb{R}$. Dobbiamo allora restringere il codominio della relazione inversa che otteniamo, in modo da ottenere una funzione vera e propria.
Definizione
Chiamiamo arcotangente la funzione $$\arctan: \mathbb{R} \rightarrow \left ( -\frac{\pi}{2}, \frac{\pi}{2} \right )$$tale che $\alpha = \arctan(t)$ sia quell’angolo compreso tra $-\frac{\pi}{2}$ e $\frac{\pi}{2}$ che soddisfa la relazione $\tan(\alpha) = t$.

Di nuovo, segnaliamo che esiste la notazione alternativa $\tan^{-1}(x)$ per questa funzione.
Infine, invertiamo la funzione $\cot(x)$:
Definizione
Chiamiamo arcocotangente la funzione $$\text{arccot}: \mathbb{R} \rightarrow \left ( 0, \pi \right )$$tale per cui $\alpha = \text{arccot}(t)$ è quell’angolo compreso tra $0$ e $\pi$ che soddisfa la relazione $\cot(\alpha) = t$.

Anche per questa funzione esiste la notazione alternativa $\cot^{-1}(x)$.
Segnaliamo inoltre che è in uso anche un’altra convenzione secondo la quale la funzione $\text{arccot}(x)$ ha come codominio $\left ( -\frac{\pi}{2}, 0 \right ) \cup \left ( 0, \frac{\pi}{2} \right ]$ anziché $(0, \pi)$. Ecco qui di seguito il suo grafico:

Le due definizioni sono quindi molto diverse:
- nel primo caso $\text{arccot}(x)$ è continua e derivabile, e nel secondo caso no;
- nel primo caso $\text{arccot}(x)$ rispetta l’uguaglianza $$\arctan (x) + \text{arccot}(x) = \frac{\pi}{2};$$nel secondo caso invece viene rispettata l’uguaglianza $$\text{arccot}(x) = \arctan \left ( \frac{1}{x} \right ), \qquad x \neq 0.$$
A seconda del contesto e delle proprietà che vogliamo siano soddisfatte, verrà utilizzata una o l’altra definizione.
In ogni caso, quello che è importante notare è che la scelta del codominio di una funzione goniometrica inversa non è assolutamente da considerare come una questione secondaria.
Ricapitoliamo quanto definito fino ad adesso.
- La funzione $\arcsin$ ha dominio $[-1, 1]$ e codominio $\left [ -\frac{\pi}{2}, \frac{\pi}{2} \right ]$, ed è la funzione tale per cui $\sin(\arcsin(x)) = x$.
- La funzione $\arccos$ ha dominio $[-1, 1]$ e codominio $\left [ 0, \pi \right ]$, ed è la funzione tale per cui $\cos(\arccos(x)) = x$.
- La funzione $\arctan$ ha dominio $\mathbb{R}$ e codominio $\left ( -\frac{\pi}{2}, \frac{\pi}{2} \right )$, ed è la funzione tale per cui $\tan(\arctan(x)) = x$.
- La funzione $\text{arccot}$ ha dominio $\mathbb{R}$ e codominio $\left ( 0, \pi \right )$ (oppure $\left ( -\frac{\pi}{2}, 0 \right ) \cup \left ( 0, \frac{\pi}{2} \right ]$), ed è la funzione tale per cui $\cot(\text{arccot(x)}) = x$.
Le funzioni goniometriche inverse soddisfano inoltre alcune interessanti identità trigonometriche. Ne riportiamo alcune qui di seguito:
##KATEX##\begin{aligned}& \arcsin (x) + \arccos (x) = \frac{\pi}{2} \\&\arctan (x) + \arctan \left ( \frac{1}{x} \right ) = \text{sgn}(x) \cdot \frac{\pi}{2} \\& \sin \left (\arccos (x) \right ) = \cos \left ( \arcsin (x) \right ) = \sqrt{1-x^2} \\& \tan \left (\arcsin (x) \right ) = \cot \left ( \arccos (x) \right ) = \frac{x}{\sqrt{1-x^2}} \\&\tan \left (\arccos (x) \right ) = \cot \left ( \arcsin (x) \right ) = \frac{\sqrt{1-x^2}}{x} \\& \sin \left ( \arctan(x) \right ) = \frac{x}{\sqrt{1+x^2}} \\& \cos \left ( \arctan(x) \right ) = \frac{1}{\sqrt{1+x^2}} \\\end{aligned}##KATEX##
La funzione $\text{sgn}(x)$ è il segno di $x$, ovvero: vale $-1$ quando $x$ è negativo, e vale $1$ quando $x$ è positivo.