Consideriamo una funzione $f$ definita su un insieme $E\subseteq Dom(f) \subseteq \mathbb{R}$. L’insieme $f(E)$ è un sottoinsieme di $\mathbb{R}$, e come tale sappiamo che ammette estremo superiore ed estremo inferiore in $\overline{\mathbb{R}}$. Quali condizioni aggiuntive dobbiamo imporre per garantire che essi siano rispettivamente massimo e minimo di $f(E)$?
Il Teorema di Weierstrass è un risultato classico dell’analisi che garantisce l’esistenza di massimo e minimo per una funzione definita e continua su un intervallo chiuso e limitato. In realtà tale risultato è valido per tutti i compatti di $\mathbb{R}$ ma qui ci limiteremo a dare enunciato, dimostrazione ed esempi di questo Teorema solo nel caso di intervalli chiusi e limitati.
Teorema (di Weierstrass): Se $f$ è una funzione reale di variabile reale, continua nell’intervallo chiuso e limitato $[a,b]\subseteq Dom(f)$, allora la funzione assume un valore minimo $m$ e un valore massimo $M$in tale intervallo: ovvero, esistono due punti $x_m, x_M \in [a, b]$ tali per cui $f(x_m)=m, f(x_M)=M$.
Dimostrazione. Prima di addentrarci nella dimostrazione, vogliamo avvisare che le tecniche di Analisi Matematica che utilizzeremo non vengono di solito approfondite alle superiori; non preoccupatevi se trovate difficile seguire il discorso, è normale!
Per prima cosa, vogliamo mostrare l’esistenza di un punto $x_M \in [a,b]$ in cui $f$ assume valore massimo $M$; una volta trovato il massimo per $f$ possiamo trovarne facilmente il minimo, vedendolo come massimo della funzione $g(x):=-f(x)$ (anch’essa continua su $[a,b]$).
Sappiamo che l’immagine di $[a,b]$ tramite $f$ ammette estremo superiore che indichiamo con $S$; inoltre, possiamo tranquillamente supporre che $S$ sia finito (in caso contrario cadrebbe la continuità di $f$). Quindi per definizione di massimo basta dimostrare che esiste un punto in $[a,b]$, il nostro $x_M$, in cui $f(x_M)=S$.
Consideriamo la successione $\{ y_n \}_{n\in \mathbb{N}}$ così definita: $$y_n = S-\frac{1}{n}.$$Questa successione è crescente e convergente a $S$. Inoltre $y_n< S$ per ogni $n$: questo ci garantisce che ogni $y_n$ non è un maggiorante per l’immagine di $f$ e quindi in $[a,b]$ esisterà sempre un $x_n$ con $f(x_n)\geq y_n$, per ogni scelta di $n$.
Consideriamo ora la successione di questi $x_n$. Non abbiamo nessuna garanzia che essa converga; però, poichè ogni $x_n$ è contenuto in $[a,b]$, la successione è limitata e grazie al Teorema di Bolzano-Weierstrass sappiamo che $\{(x_n)_{n\in \mathbb{N}}$ ammette una sottosuccessione $({x_{n_k}})_{k\in \mathbb{N}}$ convergente a un certo $x_0$ contenuto in $[a,b]’$, l’insieme derivato di $[a,b]$. Però, dato che $[a,b]$ è chiuso, si ha che $[a,b]’ = [a,b]$: possiamo quindi affermare che $x_0 \in [a,b]$. Per ciascun indice del tipo $n_k$, notiamo che vale la seguente disuguaglianza: $$y_{n_k} \leq f(x_{n_k}) \leq S. $$Possiamo allora applicare il Teorema del confronto (che qui abbiamo dimostrato essere valido per delle funzioni, ma che può essere applicato anche a delle successioni) e otteniamo $$ \lim_{k\to \infty} f(x_{n_k})=S. $$Grazie alla continuità di $f$ in $[a,b]$ abbiamo inoltre$$ \lim_{k\to \infty} f(x_{n_k})=f(\lim_{k \to \infty} x_{n_k})= f(x_0). $$Per il teorema di unicità del limite (che abbiamo dimostrato qui parlando di funzioni ma che può essere generalizzato anche nell’ambito delle successioni) deve essere necessariamente $f(x_0)=S$. Abbiamo quindi trovato un punto $x_0 \in [a,b]$ in cui la funzione ammette massimo (cioè, abbiamo appena mostrato che $x_M = x_0$).
Osservazioni sulle ipotesi del teorema di Weierstrass
Guardando l’enunciato del Teorema di Weierstrass, vediamo che sono richieste le seguenti condizioni:
- chiusura e limitatezza dell’intervallo in cui cerchiamo massimo e minimo;
- la continuità della funzione su tale intervallo.
Se alleggerissimo il teorema di una di queste ipotesi potremmo ancora garantire l’esistenza di massimo e minimo?
- Funzione non continua
Consideriamo la funzione
$$f(x):=\begin{cases}x & \text{se }x\in (-1,1)\\\frac{1}{2} & \text{se }x=-1 \vee x=1\end{cases}$$
Questa funzione non è continua in $-1$ e in $1$, e intuitivamente, si vede che essa non ammette massimo e minimo in $[-1,1]$. Il fatto che in tale intervallo non esitano massimo e minimo non contraddice affatto il Teorema di Weierstrass poiché esso come abbiamo visto richiede che la funzione sia continua. Questo esempio ci conferma che per funzioni non continue non è possibile garantire l’esistenza di massimo e minimo; essi potrebbero esistere o, come in questo caso, non esistere.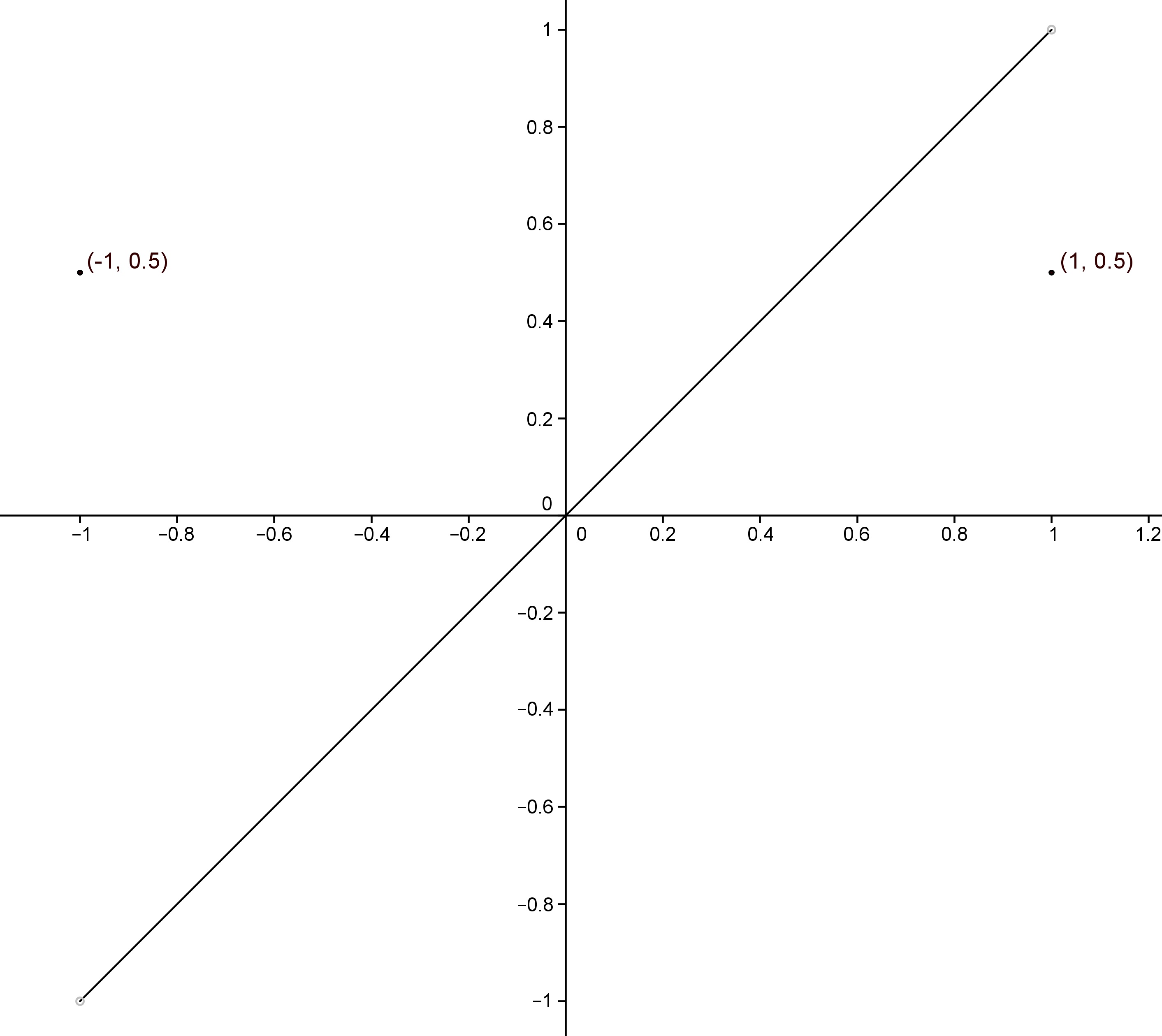
- Intervallo aperto
Consideriamo di nuovo la funzione definita nel controesempio visto prima, limitata però all’intervallo $(-1,1)$. Si vede che la funzione è continua, ma non riusciamo a individuare massimo e minimo di $f$ poiché la funzione ha codominio $(-1, 1)$ e tale insieme non ammette massimo e minimo.
Da questo deduciamo che non possiamo fare a meno di considerare un intervallo chiuso per provare ad applicare il teorema di Weierstrass. - Intervallo illimitato
Consideriamo la funzione$$f(x)=\frac{1}{x}.$$calcolata nell’intervallo $[1, +\infty)$.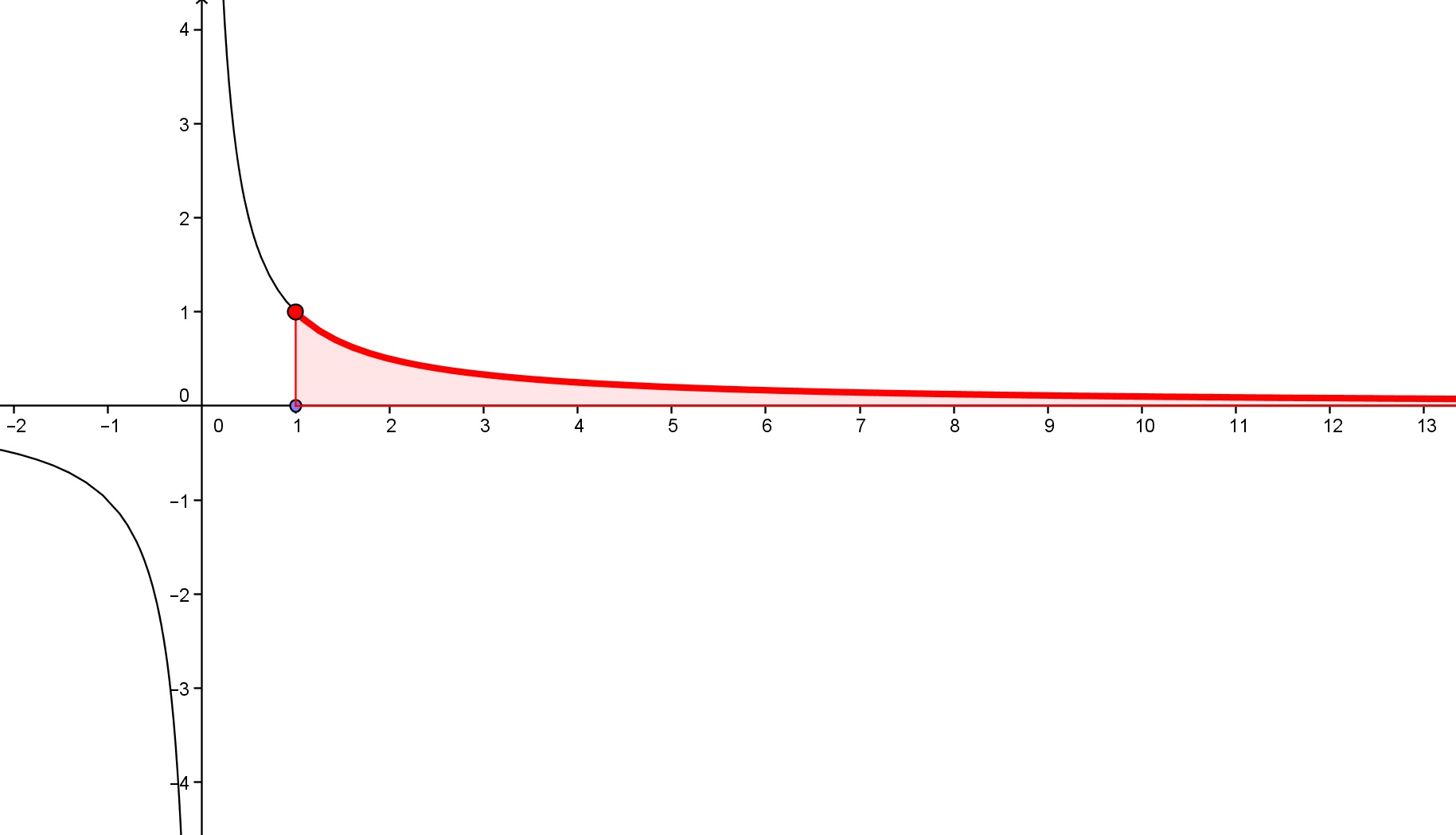
Questo intervallo è illimitato, e possiamo osservare che la funzione - pur essendo continua al suo interno - non assume un valore minimo. Questo ci fa capire che il teorema di Weierstrass non funziona quando l’ipotesi di limitatezza dell’intervallo viene a mancare.
Risolviamo adesso alcuni esercizi che riguardano la ricerca di un punto di massimo e di minimo per una funzione, utilizzando eventualmente il teorema di Weierstrass (e senza passare dallo studio dei punti stazionari).
- Consideriamo la funzione logaritmica $f(x)=\ln (x)$ ristretta all’intervallo $I=[1, e]$. Vogliamo capire se esistono massimo e minimo di $f$ in $I$, e in tal caso proveremo a determinarli.
La funzione considerata è continua sull’ intervallo $I$, che è chiuso e limitato quindi per il Teorema di Weierstrass ammette massimo e minimo. Poiché si tratta di una funzione monotona crescente, calcolando il valore della funzione agli estremi dell’intervallo otterremo il massimo e minimo di $f$ (in quell’intervallo). Abbiamo dunque ##KATEX##\begin{aligned}m &=f(1)=\ln 1=0 \\M &=f(e)=\ln e=1\end{aligned}##KATEX## - Consideriamo la funzione$$f(x)=x^2$$Essa ammette massimo e minimo in $I=[-1,2)$?
Possiamo notare che la funzione considerata è una parabola che ha minimo assoluto per $x=0\in I$, ma non assume mai un valore massimo in tale intervallo. Infatti i valori che la funzione assume in $I$ sono contenuti nell’intervallo $[0,4)$ che non ha massimo.
In questo caso non abbiamo potuto applicare il Teorema di Weierstrass perché l’intervallo $I$ non è chiuso.