Per ricavare l’equazione dell’iperbole a partire dalla definizione come luogo di punti si ricorre spesso alla semplificazione di considerare i fuochi giacenti su un asse di riferimento ($x$ oppure $y$) in posizione simmetrica rispetto all’origine. Sotto queste ipotesi ciò che si ottiene è la forma canonica dell’equazione dell’iperbole con fuochi sull'asse orizzontale: $$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1.$$ Nel caso di fuochi sull'asse verticale l'equazione si modifica come segue: $$-\frac{x^2}{a^2}+\frac{y^2}{b^2}=1.$$
Si tratta però di situazioni piuttosto restrittive, che vincolano moltissimo la nostra capacità di descrivere un’iperbole nel piano. Possiamo guadagnare una significativa dose di generalità applicando una traslazione, analogamente a quanto si può fare con altre coniche come la circonferenza, la parabola e l’ellisse.
Immaginiamo di voler traslare la nostra iperbole di un vettore $\vec v$ (disegnato in verde nella figura) di componenti $(x_0,y_0)$. Trasliamo allora gli assi cartesiani $x$ $y$ di $\vec v$ e chiamiamo $X$ e $Y$ i nuovi assi (disegnati in rosso):
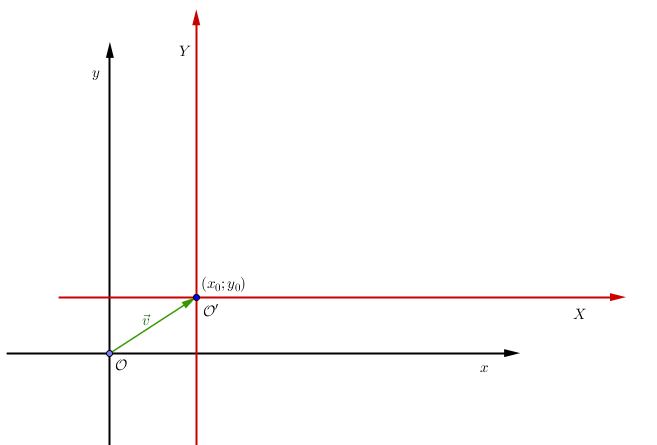
Questo significa che l’origine $\mathcal{O}’$ del nuovo sistema $\mathcal{O}’XY$ di riferimento ha come coordinate proprio $(x_0;y_0)$. Nel sistema di riferimento traslato (quello rosso per intenderci) l'iperbole ha gli assi di simmetria coincidenti con gli assi di riferimento come rappresentato dalla prossima figura.

Di conseguenza usando le coordinate $X$ e $Y$ l’equazione assume proprio la forma canonica indicata sopra: $$\frac{X^2}{a^2}-\frac{Y^2}{b^2}=1.$$
Ora, le equazioni della trasformazione sono date da $$\begin{cases} X=x-x_0 \\ Y=y-y_0 \end{cases}$$ quindi procedendo alla sostituzione di $X$ e $Y$ con le relative espressioni otteniamo l’equazione dell’iperbole traslata: $$\frac{(x-x_0)^2}{a^2}-\frac{(y-y_0)^2}{b^2}=1.$$
Proviamo a sviluppare i quadrati di binomio: $$\frac{x^2-2x\cdot x_0+x_0^2}{a^2}-\frac{y^2-2y\cdot y_0+y_0^2}{b^2}=1.$$ Ora moltiplichiamo ambo i membri per il minimo comune multiplo dei due denominatori, $a^2 b^2$ ottenendo: $$ b^2 ( x^2 - 2x \cdot x_0 + x_0^2) - a^2 (y^2 - 2y \cdot y_0 + y_0^2) = a^2 b^2$$ quindi sviluppando le parentesi, raccogliendo e riordinando i vari termini otteniamo: $$ (b^2) x^2 - (a^2)y^2 + (-2b^2x_0)x + (2a^2y_0)y +(b^2x_0^2-a^2y_0^2-a^2b^2) = 0 $$ Sembra un’espressione un po’ complicata ma dobbiamo ricordare che i parametri $a$, $b$, $x_0$ e $y_0$ in un caso specifico sono semplici numeri. Se indichiamo con $A$ e $B$ rispettivamente i coefficienti di $x$ e $y$ e con $C$ il termine noto, l'equazione risulta: $$b^2 x^2 - a^2 y^2 + Ax + By + C = 0$$ dove $A$, $B$ e $C$ sono semplici numeri reali.
L’equazione espressa in questo modo ci consente allora di riconoscere le caratteristiche che identificano un’iperbole con assi di simmetria paralleli agli assi coordinati:
- Presenza di entrambi i termini quadratici $x^2$ e $y^2$.
- Termini di secondo grado $x^2$ e $y^2$ caratterizzati da coefficienti di segno opposto.
Quindi ogni volta che in un esercizio ci viene proposta un’equazione che soddisfa queste due condizioni, possiamo immediatamente identificare la figura da essa prodotta come un’iperbole.