Nei problemi di Geometria Solida, spesso vogliamo sapere quanto misura il volume o la superficie di determinati solidi geometrici. In questa lezione riassumeremo le formule principali per determinare queste grandezze, a seconda del solido che stiamo considerando.
Prisma
Consideriamo un prisma (non necessariamente retto) e indichiamo con $B$ la misura dell’area di base, con $2p$ il perimetro di base e con $h$ l’altezza del prisma. Le misure di $B$ e $2p$ dipendono dal poligono di base del prisma che stiamo considerando e non possiamo fornire delle formule specifiche (a meno che non si tratti di un poligono regolare).

Valgono le seguenti formule:
Volume: $$V = B \cdot h.$$
Superficie laterale: $$S_{lat} = 2p \cdot h.$$
Superficie totale: $$S_{tot} = S_{lat} + 2B.$$
A partire da queste formule possiamo ricavare delle formule inverse:
Altezza: $$h = \dfrac{V}{B}, \qquad h = \dfrac{S_{lat}}{2p}.$$
Superficie di base: $$B = \dfrac{V}{h}, \qquad B = \dfrac{S_{tot} - S_{lat}}{2}.$$
Perimetro di base: $$2p = \dfrac{S_{lat}}{h}.$$
Superficie laterale: $$S_{lat} = S_{tot} - 2B.$$
Cubo
Consideriamo un cubo di lato $L$.

Valgono le seguenti formule:
Volume: $$V = L^3.$$
Superficie laterale: $$S_{lat} = 4L^2.$$
Superficie di base: $$B = L^2.$$
Superficie totale: $$S_{tot} = S_{lat} + 2B = 6L^2.$$
Diagonale: $$d = L\sqrt{3}.$$
Oltre a queste formule possiamo comunque utilizzare le formule relative a un prisma, dato che un cubo è un tipo molto particolare di prisma. Inoltre possiamo ricavare delle formule inverse per il lato del cubo:
##KATEX##\begin{aligned}& L = \displaystyle{\sqrt[3]{V}} & \quad L = \sqrt{\dfrac{S_{lat}}{4}} \\& L = \sqrt{B} & \quad L = \sqrt{\dfrac{S_{tot}}{6}} \\&L = \dfrac{\sqrt{3}d}{3}\end{aligned}##KATEX##
Piramide retta
Consideriamo una piramide retta e chiamiamo $B$ la misura dell’area di base, $2p$ il perimetro di base e $r$ il raggio della circonferenza inscritta. Indichiamo inoltre con $h$ l’altezza della piramide e con $a$ la misura del suo apotema. Come per un prisma, le misure di $B$ e $2p$ dipendono dal poligono di base della piramide che stiamo considerando.

Valgono le seguenti formule:
Volume: $$V = \dfrac{B \cdot h}{3}.$$
Superficie laterale: $$S_{lat} = \dfrac{2p \cdot a}{2}.$$
Superficie totale: $$S_{tot} = S_{lat} + B.$$
Apotema: $$a = \sqrt{r^2 + h^2}.$$
Sottolineiamo che la formula per trovare il volume sarebbe valida anche per una piramide non retta.
A partire dalle formule appena viste possiamo ricavare delle formule inverse:
Altezza: $$h = \dfrac{3V}{B}, \qquad h = \sqrt{a^2 - r^2}.$$
Apotema: $$a=\dfrac{2S_{lat}}{2p}.$$
Superficie di base: $$B = \dfrac{3V}{h}, \qquad B = S_{tot} - S_{lat}.$$
Perimetro di base: $$2p = \dfrac{2S_{lat}}{a}.$$
Superficie laterale: $$S_{lat} = S_{tot} - B.$$
Tronco di piramide
Prendiamo un tronco di piramide retta. Chiamiamo $A$ e $B$ le misure dell’area della base maggiore e minore, rispettivamente; in maniera analoga consideriamo i perimetri $2p_A$ e $2p_B$ e la misura dei raggi delle circonferenze inscritte $r_A$ e $r_B$. Indichiamo inoltre con $h$ l’altezza del tronco e con $a$ la misura del suo apotema.

Valgono le seguenti formule:
Volume: $$V = \frac{h}{3} (A + \sqrt{AB} + B).$$
Superficie laterale: $$S_{lat} = \dfrac{(2p_A + 2p_B) \cdot a}{2}.$$
Superficie totale: $$S_{tot} = S_{lat} +A+ B.$$
Apotema: $$a = \sqrt{(r_A - r_B)^2 + h^2}.$$
Otteniamo le seguenti formule inverse:
Altezza: $$h = \dfrac{3V}{A + \sqrt{AB} + B}, \qquad h = \sqrt{a^2 - (r_A - r_B)^2}.$$
Apotema: $$a=\dfrac{2S_{lat}}{2p_A + 2p_B}.$$
Superficie di base maggiore: $$A = S_{tot} - S_{lat}-B.$$
Superficie di base minore: $$B = S_{tot} - S_{lat}-A.$$
Perimetro di base maggiore: $$2p_A = \dfrac{2S_{lat}}{a} - 2p_B.$$
Perimetro di base minore: $$2p_B = \dfrac{2S_{lat}}{a} - 2p_A.$$
Superficie laterale: $$S_{lat} = S_{tot} - B - A.$$
Sfera
Consideriamo una sfera di raggio $r$.

Valgono le seguenti formule:
Volume: $$V = \frac{4}{3} \pi r^3.$$
Superficie totale: $$S = 4 \pi r^2.$$
Possiamo quindi ricavare delle formule inverse per il raggio della sfera: $$r = \sqrt[3]{\frac{3V}{4 \pi}}, \qquad r = \sqrt{\frac{S}{4 \pi}}.$$
Cilindro
Consideriamo un cilindro che ha per base un cerchio di raggio $r$ e con altezza $h$.

Valgono le seguenti formule:
Volume: $$V = \pi r^2 \cdot h.$$
Superficie laterale: $$ S_{lat} = 2 \pi r h.$$
Superficie di base: $$B = \pi r^2.$$
Superficie totale: $$S_{tot} = S_{lat} + 2B = 2 \pi r \cdot (r + h).$$
Come al solito, ricaviamo le formule inverse a partire da quello che abbiamo appena ottenuto.
Raggio di base: $$r = \sqrt{\frac{V}{\pi h}}, \quad r = \frac{S_{lat}}{2h}, \quad r = \sqrt{\frac{B}{\pi}}.$$
Altezza: $$h = \frac{V}{\pi r^2}, \quad h = \frac{S_{lat}}{2 \pi r}, \quad h = \frac{S_{tot} - 2\pi r^2}{2 \pi r}.$$
Superficie laterale: $$S_{lat} = S_{tot} - 2B.$$
Cono
Prendiamo un cono che ha per base un cerchio di raggio $r$ e di altezza $h$. Indichiamo inoltre con $a$ l’apotema del cono.

Valgono le seguenti formule:
Volume: $$V = \dfrac{\pi r^2 \cdot h}{3}.$$
Area di base: $$B = \pi r^2.$$
Superficie laterale: $$S_{lat} =\pi r \cdot a.$$
Superficie totale: $$S_{tot} = S_{lat} + B = \pi r (a + r).$$
Apotema: $$a = \sqrt{r^2 + h^2}.$$
A partire dalle formule appena viste possiamo ricavare delle formule inverse:
Altezza: $$h = \dfrac{3V}{\pi r^2}, \qquad h = \sqrt{a^2 - r^2}.$$
Apotema: $$a=\dfrac{S_{lat}}{\pi r}, \qquad a = \frac{S_{tot} - \pi r^2}{\pi r}.$$
Raggio di base: $$r = \sqrt{\frac{3V}{\pi h}}, \quad r = \sqrt{\frac{B}{\pi}}, \quad r = \frac{S_{lat}}{\pi a}.$$
Superficie laterale: $$S_{lat} = S_{tot} - \pi r^2.$$
Tronco di cono
Prendiamo un tronco di cono e chiamiamo $r$ e $R$ la misura dei raggi della base maggiore e minore, rispettivamente. Indichiamo inoltre con $h$ l’altezza del tronco e con $a$ la misura del suo apotema.
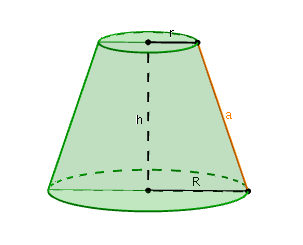
Valgono le seguenti formule:
Volume: $$V = \frac{\pi h}{3} (r^2 + rR + R^2).$$
Superficie laterale: $$S_{lat} = \pi a(r + R).$$
Superficie totale: $$S_{tot} = \pi r^2 + \pi R^2 + \pi a(r + R).$$
Apotema: $$a = \sqrt{(R - r)^2 + h^2}.$$
Otteniamo le seguenti formule inverse:
Altezza: $$h = \dfrac{3V}{r^2 + rR + R^2}, \qquad h = \sqrt{a^2 - (R - r)^2}.$$
Apotema: $$a=\dfrac{S_{lat}}{\pi (r + R)}.$$
Superficie di base maggiore: $$B = S_{tot} - S_{lat}-\pi r^2.$$
Superficie di base minore: $$B = S_{tot} - S_{lat}- \pi R^2.$$
Superficie laterale: $$S_{lat} = S_{tot} - \pi(r + R).$$
Per le formule relative ai poliedri regolari, invece, abbiamo una lezione interamente dedicata ai solidi platonici.