Prendiamo una circonferenza, e scegliamo tre o più punti su di essa. Se colleghiamo ciascuno di questi punti con il successivo (percorrendo la circonferenza in senso antiorario, per esempio) otteniamo un poligono. Che proprietà ha questo poligono? Che relazioni ha con la circonferenza da cui siamo partiti?
Più in generale, possiamo chiederci: esistono anche altre costruzioni geometriche che legano un poligono a una particolare circonferenza, o viceversa?
Definizione
Un poligono si dice inscritto in una circonferenza quando i suoi vertici stanno sulla circonferenza data. In questo caso la circonferenza si dice circoscritta al poligono.
Un poligono si dice circoscritto a una circonferenza quando i suoi lati sono tangenti alla circonferenza data. In questo caso la circonferenza si dice inscritta nel poligono.

Dato un poligono (che, come al solito, sottintendiamo sia convesso), quando possiamo trovare la circonferenza inscritta in esso? E quando quella circoscritta?
TEOREMA (Criterio di inscrivibilità di un poligono): Un poligono può essere inscritto in una circonferenza se e solo se gli assi dei lati si incontrano nello stesso punto, che è proprio il centro della circonferenza circoscritta al poligono.

TEOREMA (Criterio di circoscrivibilità di un poligono): Un poligono può essere circoscritto a una circonferenza se e solo se le bisettrici degli angoli interni si incontrano nello stesso punto, che è proprio il centro della circonferenza inscritta al poligono.

Utilizzando questi criteri, si può facilmente dimostrare che ogni poligono regolare può essere inscritto in una circonferenza e circoscritto a un’altra circonferenza, e che queste circonferenze hanno lo stesso centro.
Triangoli e quadrilateri
I teoremi enunciati nella sezione precedente valgono per un poligono generico; vale la pena di riportare alcuni risultati notevoli legati ai triangoli e ai quadrilateri.
TEOREMA: Dati tre punti nel piano, esiste sempre una unica circonferenza che li unisce.
Per il teorema precedente, possiamo sempre tracciare la circonferenza che collega i vertici di un triangolo qualunque (e il suo centro è il circocentro del triangolo). Inoltre le bisettrici degli angoli interni di un triangolo si incontrano nello stesso punto (che è l’incentro). Riassumendo, abbiamo il seguente risultato:
TEOREMA: Un triangolo si può sempre inscrivere in una circonferenza, e si può sempre circoscrivere a una circonferenza.
In particolare, ogni triangolo rettangolo può essere inscritto in una circonferenza; l’ipotenusa del triangolo è il diametro di tale circonferenza, e il suo centro è il punto medio dell’ipotenusa stessa. Per questo motivo, spesso si dice che un triangolo rettangolo è inscrivibile in una semicirconferenza.

Quando parliamo di un quadrilatero, invece, le condizioni di inscrivibilità e di circoscrivibilità possono essere ulteriormente riformulate.
TEOREMA: (Criterio di inscrivibilità di un quadrilatero): Un quadrilatero può essere inscritto in una circonferenza se e solo se due angoli opposti sono supplementari.
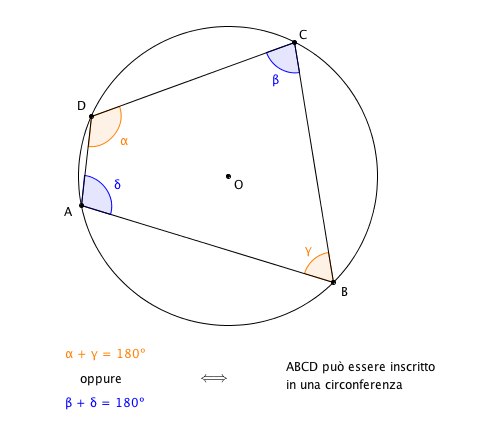
In particolare, i quadrati, i rettangoli e i trapezi isosceli sono sempre inscrivibili in una circonferenza.
TEOREMA (Criterio di circoscrivibilità di un quadrilatero): Un quadrilatero può essere circoscritto a una circonferenza se e solo se la somma di due lati opposti è congruente alla somma degli altri due.

In particolare, i rombi e i quadrati sono tutti circoscrivibili a una circonferenza.
Revisione scientifica a cura di Marco Guglielmino